Hukum-Hukum Dasar Thermodinamika
Di dalam
mempelajari thermodinamika akan selalu megacu kepada hukum-hukum dasar
thermodinamika yang ada. Ada tiga hukum yang sangat penting, yaitu
hukum thermodinamika pertama, kedua dan ketiga. Ketiga hukum ini
bersama-sama dengan hukum thermodinamika ke nol membentuk suatu dasar
yang membangun pengetahuan thermodinamika. Hukum-hukum ini bukanlah
dalil (teorema) dalam pengertian dapat dibuktikan, tetapi sebenarnya
adalah postulat yang berdasarkan kenyataan eksperimental. Seperti halnya
hukum thermodinamika pertama, suatu eksperimental telah dilakukan Joule
(1840-1878) sebagai suatu perwujudan dan pembuktian dari hukum pertama
tersebut. Dalam buku thermodinamika bagian pertama ini hanya dibahas
hukum pertama dan kedua saja.
3.1 Hukum Thermodinamika I dan Formulasinya
Hukum I
Thermodinamika menerangkan tentang prinsip konservasi energi yang
menyatakan bahwa, energi tidak dapat diciptakan dan dimusnahkan, namun
demikian energi tersebut dapat diubah dari satu bentuk ke bentuk yang
lain menjadi kerja misalnya. Dari konsep ini, dapat dikatakan bahwa
energi dapat diubah menjadi kerja dan juga kerja dapat diubah menjadi
energi. Dalam kaitan dengan Thermodinamika salah satu bentuk dari
energi yang dimaksud adalah Panas (Heat), dan kerja (Work).
Ditinjau
suatu sistem tertutup, persamaan energi di peroleh dari penyusunan
Neraca Energi untuk sistem tertutup tersebut, yaitu seperti berikut :
Keterangan : Q = Panas yang berpindah dari atau ke sistem ( Qin – Qout )
W = Kerja dalam berbagai bentuk ( Wout – Win )
Perubahan Energi total 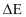 dinyatakan sebagai jumlah dari perubahan energi dalam
dinyatakan sebagai jumlah dari perubahan energi dalam 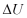 , energi potensial
, energi potensial 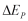 , dan energi kinetik
, dan energi kinetik 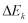 pada suatu sistem, maka persamaan (9) dapat ditulis dalam bentuk :
pada suatu sistem, maka persamaan (9) dapat ditulis dalam bentuk :
Keterangan :
kebanyakan
sistem tertutup adalah stasioner sehingga perubahan energi kinetik dan
potensial dapat diabaikan, persamaan (10) menjadi :
Telah menjadi suatu kesepakatan umum, bahwa tanda “ + “ dan “ – “ dari nilai Q dan W adalah seperti berikut ini.
Gambar 4. Sistem tertutup dan notasi kerja dan panas
Untuk menghitung nilai Kerja (W)
dari suatu proses pada sistem tertutup ini, akan diilustrasikan dari
pergerakan piston di dalam sebuah silinder, seperti gambar berikut ini.
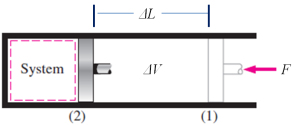
Gambar 5. Silinder Piston
Menurut Hukum thermodinamika pertama, energi dalam 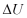 dari sistem akan berubah bila sistem akan berubah bila sistem tersebut
menerima kerja atau melepaskan panas. Dari gambar diatas dapat dikatakan
bahwa bila piston ditekan dengan tekanan tertentu secara konstan, maka
volume cairan akan berubah sampai suatu saat sistem tersebut diberikan
sejumlah kalor (panas) sehingga cairan tersebut kembali mengekspansi
sampai ke keadaan semula. Akhirnya satu siklus proses tadi dapat
dikatakan reversibel pada tekanan tetap dan volume tetap. Dalam bentuk
formulasi matematisnya dapat dinyatakan sebagai berikut.
dari sistem akan berubah bila sistem akan berubah bila sistem tersebut
menerima kerja atau melepaskan panas. Dari gambar diatas dapat dikatakan
bahwa bila piston ditekan dengan tekanan tertentu secara konstan, maka
volume cairan akan berubah sampai suatu saat sistem tersebut diberikan
sejumlah kalor (panas) sehingga cairan tersebut kembali mengekspansi
sampai ke keadaan semula. Akhirnya satu siklus proses tadi dapat
dikatakan reversibel pada tekanan tetap dan volume tetap. Dalam bentuk
formulasi matematisnya dapat dinyatakan sebagai berikut.
Kerja (W) = Gaya (F) x Jarak perpindahan (L) (12)
Untuk Gambar 5 tersebut, Gaya (F) = P x A, dimana A adalah luas penampang lintang piston yang bekerja pada cairan, dengan demikian kerja (W) dapat ditulis sebagai :
Untuk perubahan volume yang sangat kecil (dV), maka persamaan (14) dapat ditulis sebagai :
dW = P dV (15)
integrasi persamaan (15) akan menghasilkan :
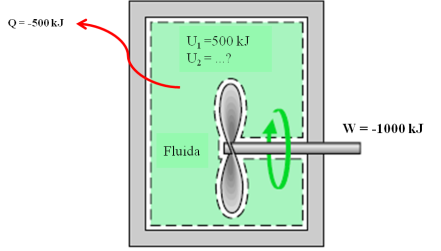
Contoh (1):
Sebuah
tangki berisi air panas yang akan didinginkan dengan cara mengaduk-aduk
air panas tersebut dengan pengaduk. Mula-mula energi dalam dari fluida
adalah 800 kJ. Selama proses pendinginan, fluida kehilangan panas
sebesar 500 kJ, dan pengaduk melakukan kerja terhadap fluida sebesar 100
kJ.Tentukan nilai energi dalam akhir.
Penyelesaian :
Persoalan tersebut digambarkan seperti berikut ini :
Gambar 6. Ilustrasi sistem
Analisis :
Terlihat
bahwa tidak ada massa yang berpindah, sehingga sistem yang dimaksud
adalah sistem tertutup atau non flow system. Tidak ada pergerakan sistem
dan sistem dianggap stasioner, sehingga DEp dan DEk sama dengan nol, maka digunakan persamaan (2-11) :
= U2 – U1
dengan mengacu pada tanda “ + “ dan “ – “ terhadap sistem, maka diperoleh :
-500 kJ – (-100 kJ) = U2 – 800 kJ
U2 = 400 kJ
2.3.2 Enthalpi
Secara eksplisit, enthalpi didefinisikan dalam bentuk persamaan matematis seperti berikut ;
H = U + PV (17)
keterangan : H = enthalpi
P = tekanan absolut
V = volume
semua
variabel yang ada dipersamaan (17) harus mempunyai satuan yang sama.
Hasil kali P dengan V mempunyai satuan energi, demikian juga dengan U.
Oleh karena U, P dan V adalah fungsi keadaan (state functions), bentuk differensial dari persamaan (17) dapat ditulis sebagai :
dH = dU + d(PV) (18)
persamaan
(18) ini digunakan apabila adanya suatu perubahan differensial pada
suatu sistem. Integrasi persamaan (18) akan menghasilkan :
enthalpi
sebagai salah satu properti thermodinamika, sangat berguna dalam banyak
pemakaian, terutama pada persoalan-persoalan yang melibatkan proses alir
yang seringkali memunculkan suku-suku U dan PV.
Contoh (2) :
Hitunglah 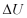 dan
dan 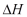 untuk 1 kg air, apabila aitr tersebut diuapkan pada temperatur konstan 100 oC
dan tekanan konstan 101.325 kPa. Volume spesifik air dalam fasa cair
dan volume spesifik air dalam fasa uapnya masing-masing adalah 0.00104
dan 1.673 m3/kg. Pada proses ini, panas sebesar 2256 kJ diberikan kepada air sehingga penguapan dapat berlangsung.
untuk 1 kg air, apabila aitr tersebut diuapkan pada temperatur konstan 100 oC
dan tekanan konstan 101.325 kPa. Volume spesifik air dalam fasa cair
dan volume spesifik air dalam fasa uapnya masing-masing adalah 0.00104
dan 1.673 m3/kg. Pada proses ini, panas sebesar 2256 kJ diberikan kepada air sehingga penguapan dapat berlangsung.
Penyelesaian :
Analisis :
air sebanyak satu kilogram ditetapkan sebagai sistem. Dimisalkan air
tersebut ditempatkan di dalam sebuah silinder tabung yang bertekanan
101.325 kPa. Begitu panas diberikan, air akan mengekspansi dari volume
mula-mula ke volume akhir, kerja yang diberikan oleh air kepada piston,
dihitung menurut persamaan (2-16), yang hasil integrasinya adalah :
W = P (V2 – V1) (A)
V2 adalah volume uap air di dalam silinder, besarnya :
= Massa air didalam tangki (volume spesifik cairan air)
= 1 kg (1.673 m3/kg)
= 1.673 m3.
V1 adalah volume air di dalam silinder, besarnya :
= Massa air didalam tangki (volume spesifik uap air)
= 1 kg (0.00104 m3/kg)
= 0.00104 m3.
Substitusikan harga-harga tersebut ke dalam persamaan (A), sehingga diperoleh :
W = (101.325 kPa) (1.673 – 0.00104) m3
W = 169.4 kPa = 169.4 kJ.
sedangkan 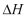 , dihitung dari persamaan (19), dengan catatan bahwa tekanan selama proses berlangsung adalah tetap, hasilnya adalah :
, dihitung dari persamaan (19), dengan catatan bahwa tekanan selama proses berlangsung adalah tetap, hasilnya adalah :
= 2087.5 kJ + 169.4 kJ = 2256.9 kJ
3.3 Proses Alir ( Flow-System) Steady-state
Untuk
kebanyakan proses dalam industri, analisis terhadap proses alir
steady-state sering dijumpai, terutama pada peristiwa mengalirnya fluida
di dalam suatu peralatan. Analisis dan perhitungan yang dilakukan
terhadap peristiwa demikian tetap akan didasari pada hukum
thermodinamika pertama dalam bentuk yang sesuai dengan kebutuhan yang
ada. Istilah steady-state dalam hal ini berkaitan dengan berlangsungnya
suatu proses tidak tergantung kepada waktu atau dengan kata lain, tidak
terjadi akumulasi massa dan energi dari suatu sistem yang ditinjau.
Sebagai dasar dari perhitungan proses alir ini, disusunlah suatu
persamaan kontinuitas.
Persamaan
kontinuitas menggambarkan suatu hubungan tekanan, kecepatan aliran, dan
luas penampang aliran dari titik inlet ke titik outlet tanpa melalui
suatu sistem peralatan proses. Berikut ini akan diturunkan persamaan
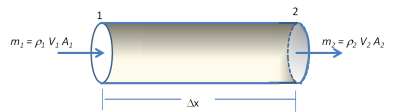
kontinuitas untuk suatu aliran satu dimensi. Sebagai Illustrasi
perhatikan Gambar 7.
Gambar 7. Aliran melalui Potongan Tabung
Apabila
proses mengalirnya fluida di dalam tabung tersebut berlangsung secara
steady-state, maka massa fluida yang mengalir melalui tiap penampang
harus sama, dengan kata lain :
Persamaan
(21) dikenal sebagai Persamaan Kontinuitas untuk aliran satu dimensi.
Dengan menggunakan differensial Logaritmik, diperoleh bentuk :
Persamaan
kontinuitas adalah pernyataan matematik dari prinsip kekekalan massa,
dan bersama-sama dengan persamaan energi sebelumnya, sangat membantu
penyelesaian soal-soal keteknikan.
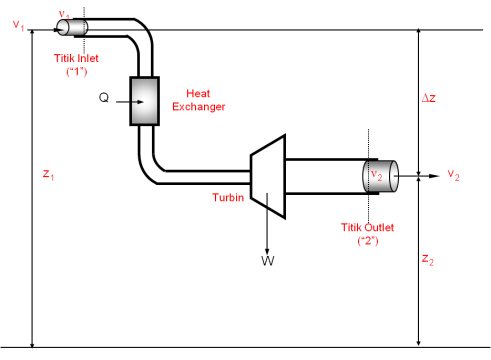
Untuk memudahkan dalam mendapatkan bentuk umum dari persamaan energi
proses alir, Pertimbangkan suatu proses alir seperti pada Gambar 8
berikut.
Gambar 8. Proses Alir Steady-state
Suatu fluida
mengalir melalui peralatan-peralatan seperti tersebut pada gambar,
dari titik inlet (“1”) ke titik outlet (“2”). Pada titik inlet (“1”)
kondisi fluida ditandai dengan subskrip 1. Pada titik ini pula fluida
berada pada ketinggian z1 dari bidang datumnya, dengan kecepatan v1, memiliki volume spesifik v1, tekanan P1 dan energi dalam (U1).
Dengan cara yang sama, untuk titik outlet ditandai dengan subskrip 2.
Sistem dianalisis dalam besaran per satuan massa fluida. Perubahan
energi per satuan massa untuk sistem tersebut melibatkan perubahan
energi kinetik, potensial dan energi dalamnya seperti pada persamaan
(10).
Keterangan :
sehingga secara umum, persamaan energi untuk proses alir steady-state dapat ditulis sebagai :
m(u2 – u1) + 1/rom(u22 – u12)+ mg(z2 – z1) = Q – W (23)
grpada persamaan (23) menyatakan semua kerja yang dilakukan oleh fluida, dan nila kerja (W) tesebut merupakan jumlah dari Kerja Poros (Shaft Work, Ws) dan Kerja hasil kali PV dari fluida yang mengalir. Yang dimaksud dengan kerja poros (Ws)
adalah kerja yang yang dilakukan atau diterima oleh fluida yang
mengalir melalui suatu peralatan sehingga dihasilkan suatu kerja mekanik
(misalnya dapat memutar suatu poros atau menggerakan baling-baling pada
turbin dan banyak lagi lainnya). Secara matematis dapat dituliskan :
W = Ws + P2V2 – P1V1 (24)
selanjutnya substitusikan persamaan (24) ke dalam persamaan (23), sehingga diperoleh :
m(u2 – u1) + 1/amm(u22 – u12)+ mg(z2 – z1) = Q – [Ws + P2V2 – P1V1] (25)
diketahui bahwa, V2 = mv2 dan V1 = mv1, dengan menyusun kembali persamaan (2-23) akan diperoleh :
m[(u F+ P2V2) –(U1 + Pil1)] + mg(z2 – z1) = Q – Ws (26)
oleh karena h = u + P V, maka persamaan (24) menjadi :
m(h2 – h1) + 1/esm(u22 – u12)+ mg(z2 – z1) = Q – Ws (27)
Persamaan (28) merupakan persamaan umum proses alir steady-state.
Untuk kebanyakan pemakaian di dalam thermodinamika, perubahan energi
kinetik dan energi potensial aliran relatif lebih kecil (sering
diabaikan) jika dibandingkan dengan energi bentuk lainnya, sehingga
persamaan (28) menjadi :
(29)
dalam hal ini, diketahui bahwa enthapi (h) adalah fungsi keadaan, sehingga ia punyai nilai tertentu pada kondisi P dan T
tertentu pula, untuk itu sering juga nilai enthalpi ini dapat dilihat
pada Tabel-tabel data thermodinamika untuk zat-zat murni tertentu.
Contoh 3 :
Udara pada tekanan 1 bar dan 25 oC
memasuki sebuah kompressor dengan kecepatan rendah, tekanan keluar
kompressor adalah 3 bar, untuk selanjutnya melewati sebuah nozel, dimana
udara tersebut akan terekspansi sehingga kecepatannya menjadi 600 m/det
dimana udara kembali pada tekanan 1 bar dan 25 oC seperti
semula. Jika pada saat kompressi terjadi adalah 240 kJ per kilogram
udara, berapa banyak panas yang dipindahkankan selama proses kompressi
tersebut berlangsung ?
x8Penyelesaian :
Analisis : oleh karena kondisi udara keluar sama dengan kondisi udara
masuk, maka dapat disimpulkan bahwa tidak ada perubahan enthalpi dari
udara. Selanjut perubahan energi kinetik mula-mula (pada titik inlet)
dapat dianggap kecil sekali. Abaikan juga perubahan energi potensial
baik pada titik inlet maupun titik outletnya, sehingga persamaan (28)
menjadi :
Q = 1/6)m(u22
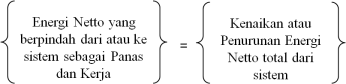
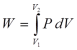
Tidak ada komentar:
Posting Komentar